01 背包

前言

异常有名的背包问题，终于有勇气面对它了。
三年前学数据结构算法的时候，那时候也不懂，参考的很多博客文章没有例子，都是数学公式生硬地出来，而且写法各种各样，导致一直没有勇气去接触这些。

题目描述

在 n 个物品中挑选若干物品装入背包，最多能装多满？假设背包的大小为 w，每个物品的大小为 A[i]

样例

样例 1:
	输入:  [3,4,8,5], backpack size=10
	输出:  9

样例 2:
	输入:  [2,3,5,7], backpack size=12
	输出:  12

动态规划

最简单的动态规划做法是将过程分为 n 个阶段，每个阶段决策是否将物品放入背包中。记住，动态规划的本质就是通过数组存储状态。

请看下面的例子，这是现在我拥有的东西以及条件

int[] weight = {2,2,4,6,3};// 物品重量
int w = 9; // 背包承受的最大重量

我们需要通过这些来构建出一个二维数组 states[n][w+1] 记录状态。states[i][j] 表示第 i 个做完决策后，背包容量 j 能放多少价值。这道题目物品的价值与物品的重量相等。

• 为什么数组是 w+1？
  数组边界可以取到 w 意味着 states[][w] 可以表示装满背包时的总价值是多大。

public int backPack2D(int m, int[] A) {
    //求出物品个数
    int n = A.length;
    int[][] states = new int[n][m + 1];
    //初始化 states[0][]
    for (int i = A[0]; i <= m; i++) {
        states[0][i] = A[0];
    }
    for (int i = 1; i < n; i++) {
        for (int j = m; j >= 0; j--) {
            //当不把物品放入背包，将上一层的数值拷贝过来
            if (states[i - 1][j] > 0) {
                states[i][j] = states[i - 1][j];
            }
        }
        //决策将物品放入背包，取最大值
        //注意这里 j 的范围
        for (int j = 0; j >= 0; j--) {
            states[i][j + A[i]] = Math.max(states[i][j + A[i]], states[i][j] + A[i]);
        }
    }
    return states[n - 1][m];
}

1. 重量数组{2,2,4,6,3}，代码更新数组如下
   new 数组时的状态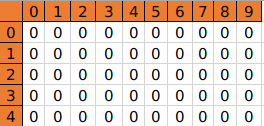

   

2. 初始化数组，第 0 个物品决策
   

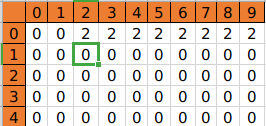
3. 第（i=1）个物品决策完后数组状态
   
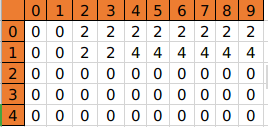
4. 第（i=2）个物品决策完后数组状态
   
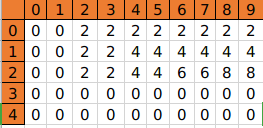
5. 第（i=3）个物品决策完后数组状态
   
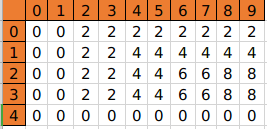
6. 第（i=4）个物品决策完后数组状态
   

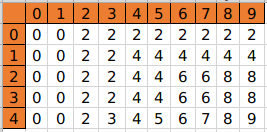
states[i][j] 表示第 i 个物品决策完后，容量为 j 的背包里最多能放多少价值的物品，所以最后返回 states[n-1][m] 即可

优化

上述解法用到了一个二维数组，其实我们还能进一步地优化空间

public int backPack(int m, int[] A) {
    int n = A.length;
    int[] states = new int[m + 1];
    for (int i = 0; i < n; i++) {
        //注意这里倒着遍历
        for (int j = m - A[i]; j >= 0; j--) {
            states[A[i] + j] = Math.max(states[A[i] + j], states[j] + A[i]);
        }
    }
    return states[m];
}

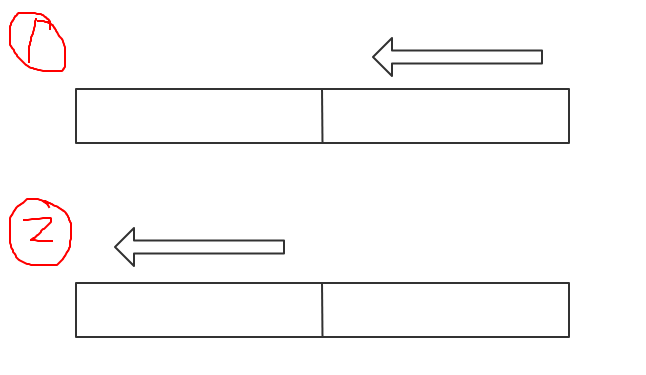
解释一下倒着遍历的那里以及 j 的范围

• 如果正序遍历，后面的值有可能直接被前面的覆盖了，当遍历到覆盖的值的时候，此时当前数组元素的值并不是从上面一行数组 copy 下来的，而是通过 max 计算出来的
• j 的范围有两种，第一种是 m 到 A[i]，可以理解为要更新的数组状态；第二种是 m-A[i] 到 0，可以理解为遍历前序数组，更新尾部的数组。虽然两种理解代码不一样，但是结果一致。
  

01 背包升级版

加上了 value 数组，我将链接以及 AC 代码贴在这里，希望对你有所帮助

• 题目链接
• 代码

  public int backPackII2(int m, int[] A, int[] V) {
      int n = A.length;
      int[] states = new int[m + 1];
      for (int i = 0; i < n; i++) {
          for (int j = m - A[i]; j >= 0; j--) {
              states[j + A[i]] = Math.max(states[j] + V[i], states[j + A[i]]);
          }
      }
      return states[m];
  }

小技巧

• 恰好装满与尽量装满
  • 恰好装满需要将数组初始化为 0,-1,-1,-1,-1……
  • 尽量装满只需要 0,0,0,0……

原因的话偷个懒，上一个背包九讲的图

总结

01 背包是动态规划的入门，需要静下心来仔细想一步步 DeBug，收获会很大。很多题目都是基于 01 背包的变种。
江湖艰险，希望此文会对你有所帮助！